Contenidos
Constante de gravitacion universal valor numerico
Valor de la constante gravitatoria universal
La constante gravitatoria (también conocida como constante gravitatoria universal, constante de gravitación newtoniana o constante gravitatoria de Cavendish),[a] denotada por la letra G mayúscula, es una constante física empírica que interviene en el cálculo de los efectos gravitatorios en la ley de gravitación universal de Sir Isaac Newton y en la teoría general de la relatividad de Albert Einstein.
En la ley de Newton, es la constante de proporcionalidad que relaciona la fuerza gravitatoria entre dos cuerpos con el producto de sus masas y el cuadrado inverso de su distancia. En las ecuaciones de campo de Einstein, cuantifica la relación entre la geometría del espaciotiempo y el tensor de energía-momento (también denominado tensor de tensión-energía).
La notación moderna de la ley de Newton que implica a G fue introducida en la década de 1890 por C. V. Boys. La primera medición implícita con una precisión de alrededor del 1% se atribuye a Henry Cavendish en un experimento de 1798[b].
Según la ley de gravitación universal de Newton, la fuerza de atracción (F) entre dos cuerpos puntuales es directamente proporcional al producto de sus masas (m1 y m2) e inversamente proporcional al cuadrado de la distancia, r, entre sus centros de masa:
El valor de la constante gravitatoria universal depende de
La constante gravitatoria (también conocida como constante gravitatoria universal, constante de gravitación newtoniana o constante gravitatoria de Cavendish),[a] denotada por la letra G mayúscula, es una constante física empírica que interviene en el cálculo de los efectos gravitatorios en la ley de gravitación universal de Sir Isaac Newton y en la teoría general de la relatividad de Albert Einstein.
En la ley de Newton, es la constante de proporcionalidad que relaciona la fuerza gravitatoria entre dos cuerpos con el producto de sus masas y el cuadrado inverso de su distancia. En las ecuaciones de campo de Einstein, cuantifica la relación entre la geometría del espaciotiempo y el tensor de energía-momento (también denominado tensor de tensión-energía).
La notación moderna de la ley de Newton que implica a G fue introducida en la década de 1890 por C. V. Boys. La primera medición implícita con una precisión de alrededor del 1% se atribuye a Henry Cavendish en un experimento de 1798[b].
Según la ley de gravitación universal de Newton, la fuerza de atracción (F) entre dos cuerpos puntuales es directamente proporcional al producto de sus masas (m1 y m2) e inversamente proporcional al cuadrado de la distancia, r, entre sus centros de masa:
Fórmula dimensional de la constante gravitatoria universal
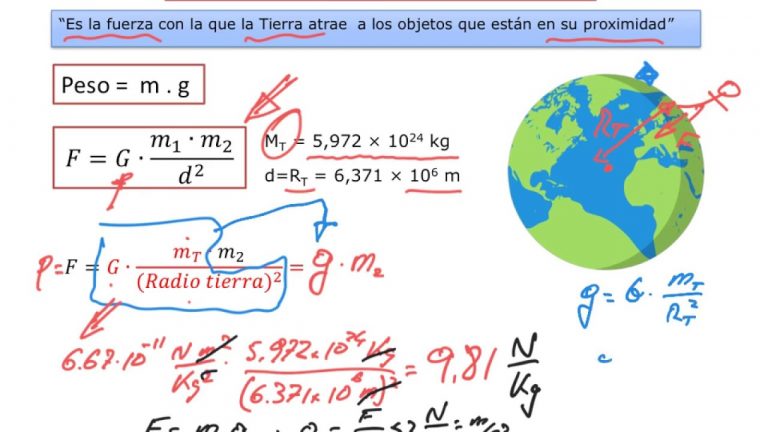
“Grande” G es la constante gravitacional de Newton y da la constante de proporcionalidad en la ley universal de gravitación de Newton que es la base de nuestra comprensión de la gravedad no relativista. La fuerza gravitatoria F entre dos cuerpos de masa m1 y m2 a una distancia R es:
Así, una manzana cae del árbol porque siente la fuerza gravitatoria de la Tierra y, por tanto, está sometida a la “gravedad”. La aceleración g=F/m1 debida a la gravedad en la Tierra puede calcularse sustituyendo la masa y los radios de la Tierra en la ecuación anterior y, por tanto, g= 9,81 m s-2.
Definir la constante gravitatoria
La constante gravitatoria (también conocida como constante gravitatoria universal, constante de gravitación newtoniana o constante gravitatoria de Cavendish),[a] denotada por la letra G mayúscula, es una constante física empírica que interviene en el cálculo de los efectos gravitatorios en la ley de gravitación universal de Sir Isaac Newton y en la teoría general de la relatividad de Albert Einstein.
En la ley de Newton, es la constante de proporcionalidad que relaciona la fuerza gravitatoria entre dos cuerpos con el producto de sus masas y el cuadrado inverso de su distancia. En las ecuaciones de campo de Einstein, cuantifica la relación entre la geometría del espaciotiempo y el tensor de energía-momento (también denominado tensor de tensión-energía).
La notación moderna de la ley de Newton que implica a G fue introducida en la década de 1890 por C. V. Boys. La primera medición implícita con una precisión de alrededor del 1% se atribuye a Henry Cavendish en un experimento de 1798[b].
Según la ley de gravitación universal de Newton, la fuerza de atracción (F) entre dos cuerpos puntuales es directamente proporcional al producto de sus masas (m1 y m2) e inversamente proporcional al cuadrado de la distancia, r, entre sus centros de masa: